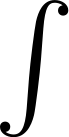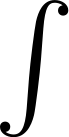
This symbol, an elongated s, represents an integral.
Integrals
From a mathematical standpoint, integrals look at the area under curves of various functions. Integrals look at specific intervals on a function and finds the area bounded by the curve and the x-axis. Integrals are very useful in the real world, offering a way to look at how rates of change affect total amounts of items. In essence, integrals are the opposite of derivatives and exactly reverse what derivatives do to a function.
What can integrals be used to find?
- Areas under curves
- Volumes of 3D objects
- Average values
- Displacement of a moving body
Integrals can also help find average values on an interval, along with also being able to help find volumes of three dimensional shapes. Integrals are able to help find a lot of values that easily apply to the real world, and in useful ways too.
| Methods of Integration | |||
|---|---|---|---|
| Substitution | Partial Fractions | Integration by Parts | |
| U-Substitution: Rewrite difficult expressions in terms of u, take the derivative for du and integrate an easier problem. |
Trig Substitution: Rewrite difficult expressions that might be hard with u-sub with trig functions to help simplify the expression and make the integration easier. |
When working with a difficult rational function, factor the denominator into simpler terms and rewrite as multiple functions that are easier to integrate. | When working with fuctions that are multiplied, split them into one part being easier to integrate and use variables u and v to represent each part, integrating v and deriving u. |
Give some feedback to help me improve this page!